IDisposable Thoughts

Ok, now we have a very simple class to make a binary tree structure and we can easily represent a tree with it, now what? well, now we are going to learn about the different ways to traverse such tree, or well, visit all the nodes in the tree. While this is not a complex operation before thinking about implementing it we have to think about what order do we want to go through all the nodes. Generally speaking there are two kind of traverse operations: depth first and breadth first traversal, both operations will traverse from top to bottom.

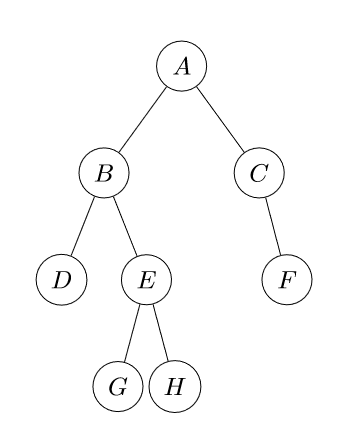
Depth-first traversal

In this mode we go from the root node and go and far as we can in each of their branches (or children). Depending on the order where the root node is visited we have three different types of depth-first traversal (the code is a method of the Node class we created in the binary tree blog post):

• Pre-order: root is visited first, then the left node and right node, in the example will be A, B, D, E, G, H, C, F

fun preOrder(operation: (T) -> Unit) {
  operation(data)
  left?.preOrder(operation)
  right?.preOrder(operation)
}

• In-order: left child first, then root and right node, in the example tree will be D, B, G, E, H, A, C, F

fun inOrder(operation: (T) -> Unit) {
  left?.inOrder(operation)
  operation(data)
  right?.inOrder(operation)
}

• Post-order: left child first, then right and root node at the end, in our tree will be D, G, H, E, B, F, C, A

fun postOrder(operation: (T) -> Unit) {
  left?.postOrder(operation)
  right?.postOrder(operation)
  operation(data)
}

You could create your own depth first traversal variations, for example, visiting right before left, the important thing here to remember is how the nodes are visited, this affects a lot the operations you will do in tree nodes (as you see in the order), one good example of different usages of each depth-first traversal is in expression evaluations.

The simple test bed for our operations is this (using the tree in the illustration and the cases we already discussed):

class TreeTraverseTests {
  private val root = Node('a',
    Node('b',
      Node('d'),
      Node('e',
        Node('g'),
        Node('h')
      )
    ),
    Node('c', right = Node('f'))
  )

  @Test
  fun `pre-order traverse`() {
    val result = mutableListOf<Char>()
    root.preOrder { result.add(it) }

    assertEquals(listOf('a', 'b', 'd', 'e', 'g', 'h', 'c', 'f'), result)
  }

  @Test
  fun `in-order traverse`() {
    val result = mutableListOf<Char>()
    root.inOrder { result.add(it) }

    assertEquals(listOf('d', 'b', 'g', 'e', 'h', 'a', 'c', 'f'), result)
  }

  @Test
  fun `post-order traverse`() {
    val result = mutableListOf<Char>()
    root.postOrder { result.add(it) }

    assertEquals(listOf('d', 'g', 'h', 'e', 'b', 'f', 'c', 'a'), result)
  }
}