IDisposable Thoughts

So far we had seen linear structures, linked list, queues, stack, arrays, all of them are linear data structures with well defined operations. Trees are our first non-linear data structure and, as the name says, they are data structures that looks like a tree (or an inverted tree).

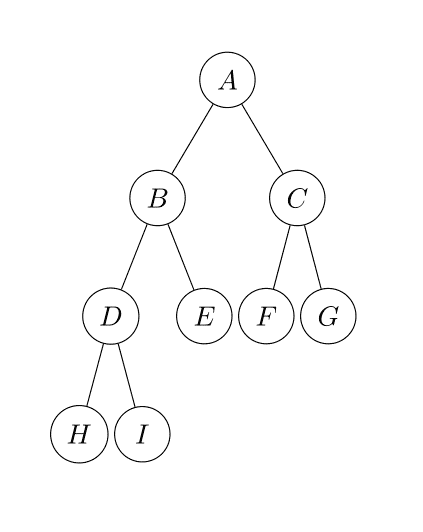
Each element in a tree is named a node and the first node, the node at the top, is named root, a node can have none or more children and each children has a parent, the “connections” between each node are called edges, nodes without children (with the exception of the root node) are called leaves, the number of edges from the root to a node is called the depth of the tree and the distance between the longest path of a node to the root is called the height of a node, so to know the height of a node or tree we count the number of nodes from that node to the root node (inclusive). In the image we see the node \(D\) has a depth of 2 and the whole tree has a height of 4, nodes \(H\), \(I\), \(E\), \(F\) and \(G\) are leaves.

`

Depending on the maximum number of children per node we have different types of trees, the simplest is a tree where each node has a maximum of 2 children (binary trees) and we will be exploring them extensively in this and upcoming blog posts. There are trees where nodes have up to three children (ternary trees) and even 4 (quaternary) and 8 (octary) trees, in general we usually talk about \(n\)-trees but we will be limiting ourselves to binary trees for now.

A simple way to assemble a binary tree is with a simple structure to hold the data and references to its left and right children, something simple like this:

class Node<T>(
    private val data: T,
    private var left: Node<T>? = null,
    private var right: Node<T>? = null
)

And we can represent a tree like the one shown in the image directly in code:

val root = Node('A',
    Node('B',
        Node('D',
            Node('H'),
            Node('I')),
        Node('E')),
    Node('C',
        Node('F'),
        Node('G'))
)

A full binary tree is a tree where all the nodes have two or no children at all, the tree in the example is a full tree. There is the concept of a complete tree but we will discuss that one when we see another structure related to trees, the heap. The maximum number of nodes in a full binary tree of \(l\) levels is given by the equation \(2^l -1\).

There are many properties of a tree that are useful when handling data, but for now try to represent a tree in your favourite language, as you see it is nothing fancy!